The Limits of LLM–Reachable Intelligence
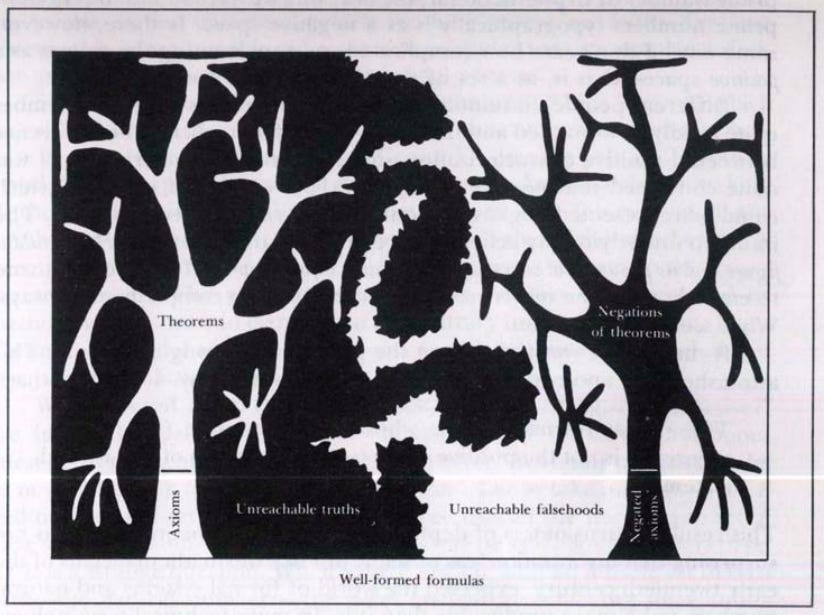
The premise of this paper is that we can do something like “map the information space”. What is reachable based on a given training corpus and what is not? How can we reach classified and proprietary information based on an unclassified corpus? These questions reminded me of this diagram from Douglas Hofstadter’s Godel Escher and Bach.
We can think of “reachable information” from LLMs as the white on the left and the axioms as the training corpus. The branches are “verifiable” “truths” within that system. What then does that say about the black space? What will be the theoretical limits of my mappings?
Even if a future LLM becomes extraordinarily capable, there is a structural limit on what it can ever certify as true. The reason is not primarily about training data, compute, or today’s model weaknesses. It is about verification. Any AI system that generates claims and is judged by a fixed, computable verifier can only ever produce a computably enumerable set of verified conclusions. Gödel-style incompleteness is a set of theorems published in 1931 by mathematician Kurt Gödel which imply that no such system can capture all truths. As applied to truth-seeking LLMs this clarifies a durable role for humans: not only to prompt models, but to design, audit, and revise the standards of verification, thereby deciding when and how system outputs are allowed to count as knowledge.
Generators and Verifiers
The paper models an AI reasoning system as a pipeline:
— Generator (M): the LLM (or any algorithm) that produces a claim plus a justification (for example, a proof, an experiment log, a string of logic).
— Verifier (V): a fixed, computable procedure that checks whether the justification is acceptable for that claim.
Examples of verifiers in practice include:
— A proof checker (Lean/Coq) that accepts only valid formal proofs.
— An experimental protocol that accepts results only if the analysis follows a pre-registered plan and meets a statistical threshold.
— A game evaluator that accepts a move only if Monte Carlo rollouts show high win rate within error bounds.
— A reward model (RLHF) that accepts outputs judged “good” by a learned scoring function trained from human preferences.
The key assumption is that the verifier is fixed and computable, meaning it always halts and outputs accept or reject.
“LLM-reachable intelligence”
Given a fixed generator and verifier, I define the reachable set as the set of claims that the model can produce together with a justification that the verifier accepts. It is not what the model can say, but what it can say and get past the check.
This matches real deployments. A model drafts a proof, a code patch, a compliance report, or a scientific claim, but a checker, test suite, or review process determines what is accepted.
Reachability is Inherently Incomplete
The argument has three steps:
1 — If the verifier is fixed, then the set of accepted claims the system can ever produce is enumerable by a program. In principle, you can list them by trying all prompts and seeds and running the verifier.
2 — Gödel’s incompleteness theorem implies that no computably enumerable system can capture all true statements.
3 — Therefore, any fixed generator paired with any fixed computable verifier will miss some truths, regardless of how powerful the generator is.
This is a structural bound: once the rules of acceptance are frozen, there will always exist true statements that never appear among the verified outputs of that system.
How Humans Can Complement AI Systems
The paper argues that the deepest human advantage over LLMs is normative flexibility:
— Mathematicians adopt new axioms when old ones prove inadequate.
— Scientists update standards when methods fail or when new instruments create new kinds of evidence.
— Communities redefine what counts as an acceptable justification.
Formally, humans can re-axiomatize. They can change the verifier over time. A fixed generator-verifier pair cannot fully capture this open-ended process.
What I do not claim
— That LLMs cannot be useful, powerful, or creative.
— Compute limits, token limits, or training data limits may not practically limit or increase reachability.
— Humans are better at arriving at truth generally.
Why this matters
This framework sets a structural bound on what even a very intelligent AI can achieve when it is paired with a fixed, computable notion of verification. It also clarifies where human value added is likely to remain. Human contribution is concentrated in deciding what counts as a valid justification, when to revise those standards, when to extend the underlying theory, and how to govern verifier updates in response to new goals, new evidence, and new failure modes. Progress is not only about building stronger generators, but about designing verification regimes and update processes that responsibly expand what the combined system can certify as true.